Welfenlab Competition 2001

Die Gewinner

Nun ist der Wettbewerb zu Ende und die Gewinner sind ermittelt. Wir möchten uns noch einmal bei allen Teilnehmern bedanken und hoffen, dass Ihr genauso viel Spass hattet wie wir.

1.Platz Lennart Baruschka, Gymnasium Mellendorf 2.Platz Florian Carstens, Leibniz Schule Hannover 3.Platz Nicolas Rott, Gymnasium Martino-Katharineum, Braunschweig Annerkennungspreise Philipp Hüger, Gymnasium am Fredenberg Karsten Schörner, Gymnasium Martino-Katharineum, Braunschweig

Schülerwettbewerb Informatik

Neuigkeiten (letzte Änderung am 25.07.2006)
Zu den 3D Daten
PDF Format

Einleitung

In der Schule lernst Du, wie man das Volumen von einfachen geometrischen Objekten (Kugel, Zylinder, Quader usw.) berechnen kann. Was ist aber mit komplizierteren Objekten, wie z.B. mit dieser Kuh?

In solchen Fällen sind meistens nur Näherungslösungen möglich. Um das Volumen zu berechnen, wird häufig die Oberfläche des Körpers durch kleine Dreiecke approximiert. Man nennt diesen Vorgang 'Triangulierung':

Das Volumen des so entstandenen Objektes kann leichter berechnet werden. Dies ist Thema des Wettbewerbs:
Es werden triangulierte Oberflächen vorgegeben, von denen u.a. das Volumen berechnet werden soll.

Und was gibt es zu gewinnen?

Unabhängig von viel Erfahrung, Ehre und Ruhm gibt es auch etwas Handfestes zu gewinnen:

1. Platz	2. Platz	3. Platz
Kodak DC5000 Zoom Digital Camera	Lexmark Optra E312L Laserdrucker	CANON CanoScan N1220U Scanner

Aufgabenstellung

Es soll ein Programm entwickelt und umgesetzt werden, das folgendes leistet:

1. Berechnung der Oberfläche triangulierter Objekte
2. a) Berechnung der größten Entfernung zwischen zwei Eckpunkten
   b) Obere Abschätzung des Volumens mit Hilfe der größten Entfernung
3. Berechnung des Volumes

Teilnahmebedingungen

• Anmeldeschluss ist der 23.10.01.
• Gruppenmeldungen sind nicht möglich.
• Als Programmiersprache sind Pascal, C, C++ und Java zugelassen. Die Sprache muss bei der Anmeldung mit angegeben werden. Es dürfen nur die Standard-Bibliotheken und keine Codegeneratoren verwendet werden.
• Es muss eine 5-10 seitige Ausarbeitung angefertigt werden, in der die benutzten Algorithmen erklärt werden und in der das Programm ausführlich dokumentiert wird.
• Das erstellte Programm und die Ausarbeitung, sowie ein Ausdruck eines Testdurchlaufs mit von uns gestellten Daten, sind spätestens bis Montag, den 07.01.02 bei uns einzureichen.
• Es dürfen nur Schüler aus dem Großraum Hannover an dem Wettbewerb teilnehmen. Familienangehörige von Mitarbeitern des Instituts für Informatik an der Universität Hannover sind leider ausgeschlossen.
• Der Rechtsweg ist ausgeschlossen.

Input-Daten

Damit Du das Dateiformat einer Triangulierung kennenlernen kannst, haben wir hier ein Beispiel eines Würfels:

<pre>Vertices:
{
(0, 0, 0); (1, 0, 0); (1, 1, 0); (0, 1, 0);
(0, 0, 1); (1, 0, 1); (1, 1, 1); (0, 1, 1)
}
Triangles:
{
{0; 1; 2}; {0; 2; 3}; {4; 5; 6}; {4; 6; 7};
{0; 1; 5}; {0; 5; 4}; {3; 2; 6}; {3; 6; 7};
{3; 0; 4}; {3; 4; 7}; {1; 2; 6}; {1; 6; 5}
}</pre>

Die Daten sind in zwei Bereiche geteilt. Das Wort Vertices: leitet eine Liste mit Punkten im ein. Die Liste, begrenzt mit geschwungenen Klammern, enthält beliebig viele Vertices (Knotenpunkte) im . Jeder Punkt besteht aus drei Koordinaten, die in einfachen Klammern stehen und mit einem Komma voneinander getrennt sind. Achtung: Jede Koordinate kann ein Dezimalbruch sein (z.B.: 2.43). Die einzelnen Punkte werden mit einem Semikolon voneinander getrennt.

Mit dem Wort Triangles: wird die Liste der Dreiecke eingeleitet. Sie enthält für jedes Dreieck auf der Oberfläche die Nummern der drei Eckpunkte aus der ersten Liste. Diese (Index-) Nummern sind natürliche Zahlen und fangen bei Null an. In diesem Beispiel hat das erste Dreieck die Eckpunkte mit den Nummern {0; 1; 2} also die Punkte (0, 0, 0), (1, 0, 0) und (1, 1, 0) im .

Auch noch wichtig: Die Zeilenumbrüche und Freizeichen sind beliebig, können also fast überall auftauchen (natürlich nicht mitten im Wort oder in einer Zahl).

So, hoffentlich haben wir Dich jetzt nicht völlig verwirrt. Am Besten Du schaust Dir das zu dem Beispiel gehörende Drahtgitterbild an:

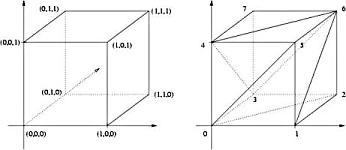
(Was mag wohl das Volumen dieses Würfels sein?).

Zum Testen solltest Du auch mal folgende Objekte ausprobieren:

Hier findest Du die 3D Daten (im Notfall kannst Du sie auch per Diskette bei uns beziehen).

Anmelden kannst Du Dich gleich hier auf der Anmeldungsseite. Außerdem gibt es hier noch den ganzen Text im PDF Format (kann man mit dem Acrobat Reader öffnen und drucken). Solltest Du es dann nicht schaffen, Dein Programm rechtzeitig abzugeben, verfällt Deine Anmeldung (sonst passiert gar nix - gibt noch nicht einmal einen Trostpreis).

Hoffentlich hast Du ein wenig Lust bekommen, bei diesem Gewinnspiel mitzumachen. Bei Rückfragen kannst Du Dich gerne bei mir melden.

E-Mail: reuter(at)gdv.uni-hannover.de

Viel Erfolg,


i.A. Dipl. - Math. Martin Reuter
Lehrstuhl Graphische Datenverarbeitung

Prof. Dr. F. - E. Wolter