Welfenlab Competition 2002

Die Gewinner

Nun ist der Wettbewerb zu Ende und die Gewinner sind ermittelt. Wir möchten uns noch einmal bei allen Teilnehmern bedanken und hoffen, dass Ihr genauso viel Spass hattet wie wir.

1.Platz
Alexander Vais, G. Büchner Gymnasium, Letter

2.Platz
Georgios C. Antonopoulos, Gymnasium Carolinum Osnabrück

3.Platz
Andreas Tarnowsky, Gymnasium Bad Nenndorf

Schülerwettbewerb Informatik

News

• Die Testdaten sind online.
• Der Anmeldezeitraum wurde verlängert. Anmeldeschluss ist nun der 15. November 2002.

Der folgende Text im PDF Format.

Worum geht es?

Aus der Schule kennst Du vielleicht schon geschlossene Polygonzüge (Vielecke, n-Ecke) in der Ebene. Es gibt geschlossene Polygonzüge ohne und mit Selbstüberschneidungen:

Geschlossene Polygonzüge

Für viele Anwendungen ist es wichtig zu wissen, ob ein Punkt im Inneren eines geschlossenen Polygonzuges liegt oder nicht.

Das ist nicht nur dann ein Problem, wenn man Polygonzüge in einem Grafikprogramm füllen will, auch moderne Grafikkarten stehen vor dieser Problematik, um möglichst schnelle 3D Darstellungen zu realisieren.

Im Falle eines geschlossenen Polygons ohne Selbstüberschneidungen ist das Problem schnell gelöst. Schwerer wird es im Fall eines geschlossenen Polygonzugs mit Selbstüberschneidungen. Man muss sich hier zunächst überlegen, wie man Innen und Aussen überhaupt definieren will.

Geschlossener Polygonzug mit Selbstüberschneidungen

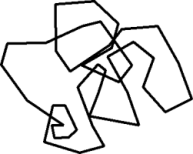Und was gibt es zu gewinnen?

Unabhängig von viel Erfahrung, Ehre und Ruhm gibt es auch etwas Handfestes zu gewinnen:

1. Platz	2. Platz	3. Platz
Pocket PC Toshiba e310	Highend AGP Grafikkarte Wert ca. 200 Euro	MP3 CD-Player Jamba

Aufgabenstellung

Es soll ein Programm entwickelt werden. In der dazugehörigen Dokumentation sollen Algorithmen und Programmaufbau verständlich dargestellt werden. Folgende Teilaufgaben sollen gelöst werden:

1. 1. Gib einen Algorithmus an, der die Anzahl der Schnittpunkte eines geschlossenen Polygonzugs (mit oder ohne Selbstüberschneidungen) mit einem Strahl, der von einem beliebigen Punkt ausgeht, bestimmt. Implementiere diesen Algorithmus.

   2. Gib einen Algorithmus an, der für einen beliebigen Punkt feststellt, ob sich dieser im Inneren eines geschlossenen Polygonzugs ohne Selbstüberschneidungen befindet, oder nicht. Implementiere diesen Algorithmus, nutze dazu den Algorithmus aus a.

   3. Gibt es einen Algorithmus, der nur mit horizontalen Strahlen arbeitet? Wenn ja, dann gib ihn an und implementiere ihn. Wenn es so einen Algorithmus nicht geben kann, dann begründe deine Antwort.

2. Betrachte die folgenden geschlossenen Polygonzüge:
   
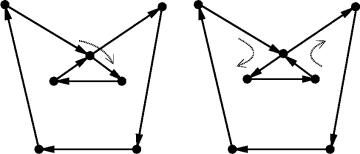
   Wie man sieht, besitzen diese Polygonzüge Selbstüberschneidungen. Gib das Innere der Polygonzüge an. Gibt es einen Unterschied? Wenn ja, erkläre den Unterschied und finde einen Algorithmus, der in beiden Fällen angibt, ob sich ein Punkt im Inneren des Polygonzugs befindet, oder nicht. Implementiere den Algorithmus.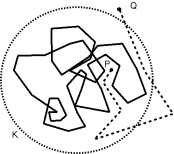

3. Zu jedem Polygonzug kann man einen Kreis K finden, der sich nicht im Inneren des Polygonzugs befindet und der den Polygonzug nicht schneidet. Man sagt, dass sich ein Punkt P im geometrischen Äußeren des Polygonzugs befindet, wenn eine Verbindung von P zu einem Punkt Q, der sich außerhalb von K befindet, existiert, die den Polygonzug nicht schneidet.
   Entwirf und implementiere einen Algorithmus zur Bestimmung des geometrischen Inneren bei beliebigen geschlossenen Polygonzügen.

Teilnahmebedingungen

• Anmeldeschluss ist der 15.11.2002.
• Gruppenmeldungen sind nicht möglich.
• Als Programmiersprache sind Pascal, C, C++ und Java zugelassen. Die Sprache muss bei der Anmeldung mit angegeben werden. Es dürfen nur die Standard-Bibliotheken und keine Codegeneratoren verwendet werden.
• Es muss eine 5 bis 10-seitige Ausarbeitung angefertigt werden, in der die benutzten Algorithmen erklärt werden, und in der das Programm ausführlich dokumentiert wird.
• Das erstellte Programm und die Ausarbeitung sowie ein Ausdruck eines Testdurchlaufs mit von uns gestellten Daten sind spätestens bis zum 10.01.2003 bei uns einzureichen.
• Es dürfen nur Schüler der Sekundarstufe I oder II einer allgemeinbildenden Schule aus Niedersachsen an dem Wettbewerb teilnehmen. Familienangehörige von Mitarbeitern des Fachgebietes Graphische Datenverarbeitung an der Universität Hannover sind leider ausgeschlossen.
• Der Rechtsweg ist ausgeschlossen.

Input-Daten

Für einen Polygonzug ist folgendes Dateiformat zu benutzen:

<pre>Polygon:
{
(0.5, 1); (5.07, 6.2); (6,7); (1, 5);(5, 4); (2, 6);
(6 ,7); (0, 4); (4 , 7); (2, 6) ; (6, 5)
}
Testpoints:
{
(5.5, 5.5) ; (3.33 , 4.66) ; (0,0)
}</pre>

Wie Du siehst, besteht so eine Datei aus zwei Listen mit 2D Punkten. Die erste Liste beschreibt das Polygon, die zweite enthält Testdaten, also 2D Punkte die für die Innen-Außen-Tests in allen drei Aufgaben benutzt werden sollen.

Da wir grundsätzlich geschlossene Polygonzüge betrachten, wird der letzte angegebene Polygonpunkt automatisch mit dem ersten Polygonpunkt verbunden. Also bitte nicht den ersten Punkt am Ende noch einmal angeben! Grundsätzlich wird nach dem letzten Punkt kein Semikolon angegeben.

Auch noch wichtig: Die Zeilenumbrüche und Freizeichen sind beliebig, können also fast überall auftauchen (natürlich nicht mitten im Wort oder in einer Zahl).

Zum Testen wird es einige Dateien auf unserer Webseite geben (im Notfall kannst Du sie auch per Diskette bei uns beziehen).

Anmelden kannst Du Dich im Internet oder per Post mit dem beiliegenden Anmeldebogen. Solltest Du es dann nicht schaffen, Dein Programm rechtzeitig abzugeben, verfällt Deine Anmeldung (sonst passiert gar nix - gibt noch nicht einmal einen Trostpreis).

So das war's erstmal. Hoffentlich hast Du ein wenig Lust bekommen, bei diesem Gewinnspiel mitzumachen. Bei Rückfragen kannst Du Dich gerne bei mir melden.

E-Mail: competition(at)gdv.uni-hannover.de

Viel Erfolg,


i.A. Dipl. - Math. Martin Reuter
Lehrstuhl Graphische Datenverarbeitung

Prof. Dr. F. - E. Wolter