Welfenlab Competition 2005
Aktuell
03.07.2006 09:53
- Platz: Christian Hoffmeister, Schillerschule Hannover
- Platz: Jan Gosmann, Bismarckschule Hannover
- Platz: Andre Ryll, Fachgymnasium Technik Oldenburg
Anerkennungspreise (alphabetisch)
- Sebastian Albert, Hölty-Gymnasium Celle
- Martin Binder, Leibnizschule Hannover
- Ilya Elenski, KGS Ronnenberg
- Maximilian Klein, Georg Büchner Gymnasium Letter
- Timo Nachstedt, Matthias-Claudius-Gymnasium Gehrden
26.01.2006 17:55 Neue Beispieldateien
Es sind jetzt zwei neue Beispieldateien online.
Schülerwettbewerb Informatik
Wir, d.h. der Lehrstuhl Graphische Datenverarbeitung in der Fakultät Elektrotechnik und Informatik veranstalten für Schüler an niedersächsischen Gymnasien einen Wettbewerb im Bereich der Computergeometrie. Wir nennen unser Fachgebiet Welfenlab, nach dem Hauptgebäude der Universität, dem Welfenschloss, daher der Name "Welfenlab Competition". Bisher fand der Wettbewerb viermal statt und auch in diesem Jahr gibt es ihn wieder.
Anmeldung
Die Teilnahmebedingungen stehen am Ende dieser Seite.
Worum geht es?
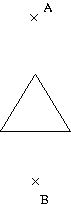
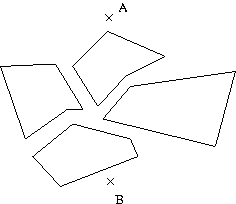
Nachdem wir uns in den letzten Jahren mit Knoten und ihren Eigenarten beschäftigt haben, widmen wir uns dieses Mal der Graphentheorie. Ein Graph ist dabei sehr theoretisch, man kann ihn jedoch durchaus zur Lösung ganz realer Probleme einsetzen. Dazu ein kleines Beispiel: Wir wollen in der Abbildung 1 links vom Punkt A den kürzesten Weg zum Punkt B bestimmen. Ungünstigerweise ist der direkte Weg versperrt, in diesem einfachen Beispiel ist einer der beiden kürzesten Wege jedoch problemlos durch hinschauen zu erkennen. In der Abbildung in der Mitte ist dies nicht mehr so einfach. Um gar auf einer Land- oder Stadtkarte den kürzesten Weg zu finden braucht man entweder viel Zeit oder einen Algorithmus, den auch ein Computer beherrscht. Um dem Computer unser Problem zugänglich zu machen und es gleichzeitig zu verallgemeinern, transformieren wir unsere Umgebung (hier eine Art Landkarte) in einen Graphen. Wir suchen also kürzeste Wege in einem Graphen.
|
|
|
Abbildung 1: zwei relativ einfache Szenarien und ein Beispielgraph
Ziel der Competition ist es, ein Programm zu schreiben, das gewisse vorgegebene Szenarien in einen Graph transformiert, um in diesem Graph das Kürzeste-Wege-Problem mittels eines bereits bekannten Algorithmus zu lösen. Der kürzeste Weg im Graph entspricht dann dem kürzesten Weg im Szenario.
Und was gibt es zu gewinnen?
Unabhängig von viel Erfahrung, Ehre und Ruhm gibt es auch etwas Handfestes zu gewinnen:
| 1. Platz: | 2. Platz: | 3. Platz: |
|
|
|
Digicam | mp3-Player | Lautsprecher |
Hintergrund
Als Kürzeste-Wege-Problem dient uns ein Szenario, das einer Landkarte ähnelt. Wir haben einen Startpunkt und einen Zielpunkt. Weiterhin gibt es Hindernisse, die wir nicht überwinden können. Um ein solches Szenario zu speichern,benötigen wir eine Art Szenariodatei. In dieser Datei stehen alle nötigen Informationen, d.h. die Koordinaten der Start- und Zielpunkte und die Lage der Hindernisse, die bei uns durch geschlossene Polygone repräsentiert werden. (Ein geschlossenes Polygon ist eine Menge von Punkten bei denen jeder mit dem nächsten und der letzte mit dem ersten Punkt verbunden sind. Unsere Polygone haben keine Selbstüberschneidungen.) Um das Problem noch ein wenig komplexer zu machen, führen wir noch sogenannte Beamspots ein, an denen man sich zu einem anderen Spot beamen lassen kann. Beamspots treten immer gruppenweise auf (d.h. mindestens zwei), und innerhalb einer Gruppe kann man von jedem Spot zu jedem anderen reisen. Das folgende Beispiel zeigt eine solche Datei und das zugehörige Szenario.
<pre>A = 5.0 9.0 (Startpunkt)
B = 5.0 1.0 (Endpunkt)
P = 3.0 5.0;5.0 6.0;7.0 5.0 (dreieckiges Polygon als Hindernis)
P = ... (evtl. weitere Hindernisse)
BS = 1.0 9.0;9.0 1.0 (Gruppe von Beamspots)
BS = ... (evtl. weitere Beamspots)</pre>
 |  |
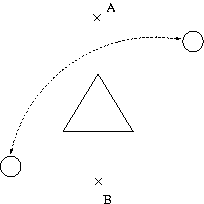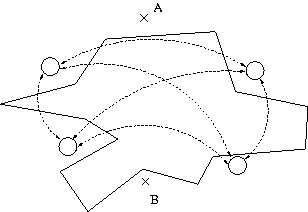Abbildung 2: zwei denkbare Szenarien mit Beamspots
Selbstverständlich brauchen wir auch ein Dateiformat, um einen gewichteten Graphen abzuspeichern. Anhand des folgenden Beispiels sollte die Struktur klar sein. Die in der ersten Zeile angegebenen Ecken werden durchnummeriert beginnend bei 1.In der Datei wird im Weiteren die Nummer als Identifikation für die Ecke benutzt. Die Koordinaten der Ecken werden nur der Form halber mit abgespeichert.
<pre>5.0 9.0;5.0 1.0;3.0 5.0;5.0 6.0 (Koordinaten der Eckpunkte)
1 3 3.0 (Kante von 1. zu 3. Ecke mit Gewicht 3)
3 4 2.0 (Kante von 3. zu 4. Ecke mit Gewicht 2)
... (evtl. weitere Kanten)</pre>
Weitere Beispiele für Szenario- und Graphendateien:
Aufgabenstellung
Es soll ein Programm entwickelt werden. In der dazugehörigen Dokumentation sollen Algorithmen und Programmaufbau verständlich dargestellt werden. Folgende Teilaufgaben sollen gelöst werden:
- Überleg dir, wie man überprüft ob eine Strecke ein Polygon schneidet. Entwickle daraus einen Algorithmus. Als Eingabe erhält der Algorithmus ein geschlossenes Polygon und zwei Ecken (siehe Szenariodatei), und als Ausgabe erhält man die Antwort ob die direkte Verbindung der beiden Ecken das Polygon schneidet oder nicht. Dokumentiere deine Überlegungen und dein Vorgehen und beachte, dass der Algorithmus möglichst schnell/effizient ist, da er in der nächsten Teilaufgabe viel benutzt wird.
- Entwickle einen Algorithmus der als Eingabe eine Szenariodatei erhält, diese einliest und als Ausgabe eine Graphendatei liefert und diese speichert. Dabei ist folgendes Vorgehen sinnvoll, damit sich ein Graph ergibt, der unser Szenario repräsentiert.
- Start-, End- und jeder Eckpunkt eines Polygons wird zu einer Ecke im Graph.
- Zwischen zwei Ecken gibt es genau dann eine Kante falls es im Szenario möglich ist eine direkte Verbindung zu ziehen, ohne ein Hindernis, d.h. ein Polygon zu schneiden. Die Kante erhält als Gewicht bzw. Kosten die Entfernung der Punkte im Szenario.
- Überlege dir und begründe warum dieses Vorgehen zweckmäßig ist
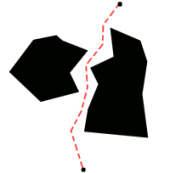
Abbildung 3: Transformation eines Szenarios in einen Graphen. - Es soll der kürzeste/billigste Weg in einem Graph gefunden werden. Da dieses Gebiet bereits gut erforscht ist wollen wir uns einiger Ergebnisse bedienen. Der Dijkstra-Algorithmus ist ein Algorithmus, der den kürzesten Weg in einem Graphen anschaulich konstruiert. Er ist relativ einfach, und es gibt sehr gute Beispiele im Internet:
- http://de.wikipedia.org/wiki/Dijkstras_Algorithmus
- http://www.mcgods.de/fun/1904/node8.html
- http://www.gik.uni-karlsruhe.de/766.html
- Nachdem wir es geschafft haben den kürzesten Weg in sehr komplexen Szenarien zu bestimmen, wollen wir versuchen unsere Fragestellungen ein wenig zu verallgemeinern und fragen nun nach dem Weg vom Start- zum Zielpunkt mit minimaler Winkelsumme. Diese ergibt sich durch Aufaddieren aller beim Übergang von einer Kante zu einer anderen auftretenden Winkel, die sich durch die Richtungsänderung ergeben. Als Beispiel betrachte man folgende Abbildung rechts in denen zwei Wege (einmal als durchgezogene und einmal als gestrichelte Linie) eingezeichnet sind.
Abbildung 4: Messen der Winkelsummen
Der Weg mit der höheren Winkelsumme ist der zackigere Weg. Wir wollen also einen möglichst wenig zackigen Weg finden. Bei genauem Vergleich der Problemstellungen fällt auf, dass es sich wiederum um ein Minimierungsproblem in einem Graphen handelt. Es stellt sich die Frage, inwiefern unser bisheriges Vorgehen geeignet ist, um auch den Weg mit minimaler Winkelsumme zu bestimmen. Entwickle analog zum Vorgehen in den Teilaufgaben 1 bis 3 einen Algorithmus, der zu einer gegebenen Szenariodatei den Weg mit der geringsten Winkelsumme findet. Falls es mehrere gibt sollen selbstverständlich alle ausgegeben werden.
Benutzt man einen Beamspot, guckt man nach dem Beamen in die gleiche Richtung wie vorher, d.h. Beamspots verkürzen zwar den Weg enorm, die Winkelsumme aber eventuell nicht.
Vergleiche nun bei gleicher Szenariodatei die Ergebnisse des kürzesten Weges und der minimalen Winkelsumme. Was lässt sich sagen, falls Beamspots beteiligt sind? Was, wenn nicht? Halte deine Ergebnisse fest und begründe deine Schlussfolgerungen oder liefere Gegenbeispiele.
Teilnahmebedingungen
- Anmeldeschluss ist der 30. November 2005.
- Gruppenmeldungen sind nicht möglich.
- Als Programmiersprache sind Pascal, C, C++ und Java zugelassen. Die Sprache muss bei der Anmeldung mit angegeben werden. Es dürfen nur die Standard-Bibliotheken und keine Codegeneratoren verwendet werden.
- Es muss eine 5 bis 10-seitige Ausarbeitung angefertigt werden, in der die benutzten Algorithmen erklärt werden, und in der das Programm ausführlich dokumentiert wird.
- Das erstellte Programm und die Ausarbeitung sowie ein Ausdruck eines Testdurchlaufs bzw. die Ergebnisse mit von uns gestellten Daten sind spätestens bis zum 20. Februar 2006 bei uns einzureichen. Es ist möglich anstelle eines Ausdrucks die Dokumente auch als PDF mit dem Programm per Mail abzugeben.
- Es dürfen nur Schüler der Sekundarstufe I oder II an allgemeinbildenden Schulen, sowie an Fachgymnasien aus Niedersachsen an dem Wettbewerb teilnehmen. Die Teilnehmer dürfen max. 19 Jahre alt sein. Familienangehörige von Mitarbeitern des Fachgebietes Graphische Datenverarbeitung an der Universität Hannover sind leider ausgeschlossen.
- Der Rechtsweg ist ausgeschlossen.
Bewertungskriterien
- Lauffähigkeit und Korrektheit des Programms
- Gut verständliche Dokumentation der Algorithmen, ggf. mit Ergebnissen von Beispieldaten
- Besondere eigenständige Ideen
- In Zweifelsfällen: Strukturierter Programmierstil
So, das war's erstmal. Hoffentlich hast Du ein wenig Lust bekommen, an diesem Wettbewerb teilzunehmen. Es geht bei dieser Competition nicht darum, alles perfekt zu machen. Wir freuen uns auch über Teillösungen. Wenn wir merken, dass Du Dich mit der Problematik beschäftigt hast, hier und da ein paar interessante eigene Ideen hattest und Deine Gedanken und Algorithmen dokumentierst, hast Du gute Chancen unter den Besten zu sein. Bei Rückfragen kannst Du Dich gerne bei uns melden.
E-Mail: competition(at)gdv.uni-hannover.de
Viel Erfolg,
Hannes Thielhelm
Dipl.-Math. Dennis Allerkamp
Prof. Dr. F.-E. Wolter
Lehrstuhl Graphische Datenverarbeitung
