Spectral Surface Quadrangulation
Dr. Peer-Timo Bremer, Leibniz Universität Hannover,
Seminar
11/2006
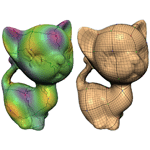 Resampling raw surface meshes is one of the most fundamental operations used by nearly all digital geometry processing systems. The vast majority of this work has focused on triangular remeshing, yet quadrilateral meshes are preferred for many surface PDE problems, especially fluid dynamics, and are best suited for defining Catmull-Clark subdivision surfaces.
Resampling raw surface meshes is one of the most fundamental operations used by nearly all digital geometry processing systems. The vast majority of this work has focused on triangular remeshing, yet quadrilateral meshes are preferred for many surface PDE problems, especially fluid dynamics, and are best suited for defining Catmull-Clark subdivision surfaces.
We describe a fundamentally new approach to the quadrangulation of manifold polygon meshes using Laplacian eigenfunctions, the natural harmonics of the surface. These surface functions distribute their extrema evenly across a mesh, which connect via gradient flow into a quadrangular base mesh.
An iterative relaxation algorithm simultaneously refines this initial complex to produce a globally smooth parameterization of the surface. From this, we can construct a well-shaped quadrilateral mesh with very few extraordinary vertices.The quality of this mesh relies on the initial choice of eigenfunction, for which we describe algorithms and heuristics to efficiently and effectively select the harmonic most appropriate for the intended application.
Contact:

