Auffinden ähnlicher Flächen durch den Laplace-Beltrami-Operator
Richard Guercke, Leibniz Universität Hannover,
bachelor thesis
09/2005
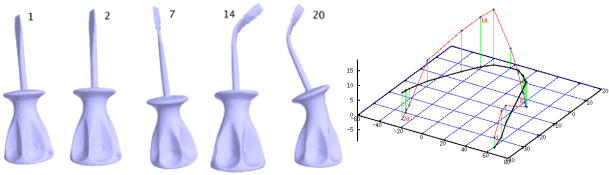
Die beiden obigen Bilder zeigen Zwischenstufen der Verformung des 3d-Modells eines Schraubenziehers und die Entwicklung der zugehörigen Spektra (projiziert in den dreidimensionalen Raum).
Das Problem, eine leicht verformte und eventuell auf verschiedene Weise dargestellte (Bezier-, B-Spline-Darstellung, trianguliert,...) oder umparametrisierte Fläche in einer Sammlung von Flächen wiederzufinden, hat insbesondere im Zusammenhang mit Patentrechtsverletzungen oder bei der Identifikation von Objekten eine wichtige Bedeutung. Aufgrund der Vielzahl der möglichen Darstellungsformen und Parametrisierungen ist dieses Problem ohne aufwendige Vorbereitungsschritte nur schwer lösbar.
Die Berechnung der Eigenwerte des Laplace-Beltrami-Operators bildet eine Fläche auf eine Menge von Zahlen ab, wobei hier nur die ersten (kleinsten) k - typischerweise 50 bis 500 - Eigenwerte benutzt werden.
Diese Zahlen lassen sich als die Frequenzen der Eigenschwingungen des betreffenden Objektes interpretieren. Dieser (materialunabhängige) "Ton" bei der Anregung eines Objektes zu einer Eigenschwingung dient als "Fingerabdruck" für die Fläche, anhand dessen Flächen auf Ähnlichkeit geprüft und in Sammlungen eingeordnet werden können.
Theoretische Überlegungen und praktische Versuche zeigen, dass der Abstand zwischen den k-dimensionalen Punkten, die durch die (aufsteigend sortierten) ersten k Eigenwerte beschrieben werden, ein sinnvolles Maß für die Ähnlichkeit der zugehörigen Flächen ist. So lässt sich die Suche nach ähnlichen Flächen in einer Sammlung auf die Suche nach nächsten Nachbarn von Punkten im k-dimensionalen Raum zurückführen.
In dieser Arbeit wurden einerseits weitere Untersuchungen zur Entwicklung der Laplace-Spektra bei der Verformung von Objekten angestellt und andererseits verschiedene Versuche zum Informationsverlust bei der Anwendung der Principal Component Analysis (Projektion der hochdimensionalen Punkte auf die Achsen ihrer größten Varianz) auf Mengen von Spektra zur Verringerung der Dimensionalität durchgeführt.
Kontakt: Martin Reuter

