Zerlegung polygonal berandeter Gebiete in der euklidischen Ebene in konvexe Teilbereiche

Daniela Lauer, Leibniz Universität Hannover, bachelor thesis
01/2005

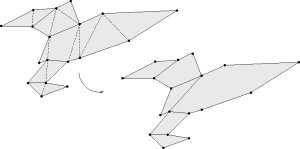
In der Computergrafik werden möglichst einfache Darstellungen verwendet um geometrische Objekte zu modellieren. Eine gängige Methode ist es ein Objekt durch die Approximation seiner Oberfläche darzustellen. Dabei wird diese aus einer Menge planarer Vielecke,

 

hier Polygone genannt, zusammengesetzt. Damit auch komplexe Objekte effektiv verwaltet und bearbeitet werden können, wird jedoch noch eine einfachere Darstellung der Teilstücke benötigt. Eine Möglichkeit ist, Polygone als die Vereinigung von weniger komplexen Teilstücken zu repräsentieren. Ein konvex zerlegtes Polygon setzt sich nur aus konvexen Teilstücken (einfacheren Polygonen) zusammen.

Die Motivation für die vorliegende Arbeit kommt aus der Computergrafik aus dem Gebiet wissenschaftliche Visualisierung mit Spiele-Engines. Für eine optisch anspruchsvolle Visualisierung in Echtzeit wird unter anderem eine leistungsstarke Renderingsoftware benötigt. Eine günstige Alternative zu kommerziellen Produkten wie z.B. 3D Studio MAX oder Autocad bieten Spiele-Engines. Im Gegensatz zu den Anfängen der Computergrafik sind heute die Hersteller von animierten Filmen und Computerspielen führend im Bereich der Echtzeit 3D-Visualisierung.

Deshalb wird am Lehrstuhl Graphische Datenverarbeitung, Institut für Mensch-Maschine-Kommunikation der Leibniz Universität Hannover, die Eignung von Spieleengines für die Visualisierung wissenschaftlicher Daten anhand einiger Beispiele (Sarnow: Quake 3, Hanel: Unreal 2) erprobt. Die von einem Laserscanner gemessene Punktwolke der Höhlenwände wurde in Diplomarbeiten (Farajollahi, Friese,) in eine triangulierte Darstellung überführt und dient als Datenquelle für diese Untersuchungen. Erste Ergebnisse ermöglichen ein flüssiges Durchwandern der Höhle. In der Darstellung mit der Quake-Engine führte jedoch beispielsweise das Hinzufügen von aufwändigen Lichteffekten zu Performanceverlusten. Dies liegt unter anderem an der Menge der darzustellende Polygone (bislang Dreiecke). Die Quake Engine ist jedoch in der Lage, nicht nur Dreiecke, sondern konvexe Polygone einzulesen und zu verarbeiten. Dies eröffnet die Möglichkeit, durch das Verwenden größerer konvexer Teilstücke mit möglichst wenig Detailverlust die Anzahl der Polygone zu reduzieren.

Die Idee liegt also nahe, nach großen planaren oder quasiplanaren Teilgebieten bestehend aus mehreren Dreiecken zu suchen, um diese dann als Vereinigung einer Menge von konvexen Polygonen darzustellen. Es wird also ein Algorithmus benötigt, der ein in triangulierter Form vorliegendes Gebiet (Polygone) in möglichst wenige konvexe Teilstücke zerlegt.

Kontakt: Karl-Ingo Friese