Welfenlab Competition 2003
SchÞlerwettbewerb Informatik
Resonanz
Die Welfenlab Competition 2003 ist nun beendet und die PreistrÃĪger des Wettbewerbs wurden im Rahmen der Ada Lovelace Memorial Celebration geehrt. Die Gewinner sind:
1.Platz
Oliver MÞller , NiedersÃĪchsisches Internatsgymnasium Bad Harzburg
2.Platz
Steffen Matthias, Gymnasium Bad Nenndorf
3.Platz
Ulrich v.d. Ohe, Otto-Hahn-Gymnasium Springe
Dariush Forouher, Bernhard-Riemann-Gymnasium Scharnebeck
Anerkennungspreise
Marc RÃķhrig, Philipp Kleybolte (beide Leibnizschule Hannover), Michael Siebert (Halephagen-Schule Buxtehude), Andre Ryll (Oldenburg)
Wir hoffen, dass alle Teilnehmenden genauso viel Spass hatten wie wir und freuen uns Þber die positive Resonanz:
Bericht der Leibnizschule Hannover
Bericht der Halepaghen-Schule Buxtehude
Organisatorisches
Wir haben den folgenden Text und das Anschreiben, welches wir an verschiedene Schulen geschickt haben, auch im PDF Format:
- die Beschreibung,
- das Anschreiben.
Testdaten
Einige Testdaten sind jetzt online abrufbar. Es gibt folgende DatensÃĪtze:
- 2-Doppelkringel
- 2.5-Doppelkringel
- 4-Kringel
- 5-Kringel
- komplizierte Schlinge
Worum geht es?
Die Aufgabe dieser Competition kommt aus dem spannenden und noch nicht besonders gut erforschten Gebiet der Knotentheorie. Was ein Knoten ist, weiss so ziemlich jeder, der schon mal beim Ãffnen der Schleife am Schuh an einem Ende gezogen hat, das dummerweise durch eine der Schlaufen verlief. Allerdings lassen sich solche Knoten entknoten (da ja beide Enden einfach nur entlang ihrem Verlauf im Knoten zurÞckgefÞhrt werden mÞssen). Daher betrachten wir auch nur FÃĪlle, bei denen die beiden Enden miteinander verbunden sind, also geschlossene Knoten:
 |  |
Den Wissenschaftlern stellt sich dabei die Frage, ob ein gegebener Knoten entknotbar ist, also ob er sich auf den sogenannten Unknoten (Abb. 1a) zurÞckfÞhren lÃĪsst. Der Trefoil aus Abb. 1b lÃĪsst sich z.B. nicht entknoten. Auch die Verknotung (Abb. 2a und 2b) eines DNS-MolekÞls unter dem Elektronenmikroskop ist nicht der Unknoten.
 |  |
Abbildung: 2 a) DNS MolekÞl b) zugehÃķriger Knoten | |
Ziel dieser Competition ist es, ein Programm zu schreiben, das Knoten einlesen, konvertieren und vereinfachen kann. AuÃerdem soll festgestellt werden, ob zwei Knoten miteinander verlinkt sind, oder ob sie sich ohne Aufschneiden voneinander trennen lassen. Doch mehr dazu spÃĪter ...
Und was gibt es zu gewinnen?
UnabhÃĪngig von viel Erfahrung, Ehre und Ruhm gibt es auch etwas Handfestes zu gewinnen:
| 1. Platz | 2. Platz | 3. Platz |
|---|---|---|
 |  |  |
| 17'' Flachbildschirm | DVD-Brenner | USB Stick |
| NEC LCD1760NX o.ÃĪ. | Plextor PX-708A o.ÃĪ. | USB 2.0 256MB |
Hintergrund
Da die zu Anfang beschriebenen Knoten beliebig komplex werden kÃķnnen, wollen wir uns im weiteren Verlauf der Competition mit der "Verlinkungsfrage" bei einfachen "Links" beschÃĪftigen. Ein Link besteht aus zwei geschlossenen Knoten, die entweder voneinander getrennt werden kÃķnnen, d.h. separierbar sind (siehe Abb. 3a) oder nicht (dann sind sie verlinkt, siehe Abb. b):
 |  |
| Abbildung 3: a) Separierbar b) Verlinkt |
Aufgabenstellung
Es soll ein Programm entwickelt werden. In der dazugehÃķrigen Dokumentation sollen Algorithmen und Programmaufbau verstÃĪndlich dargestellt werden. Folgende Teilaufgaben sollen gelÃķst werden:
Einlesen eines geschlossenen Kantenzuges aus einer Datei. Dabei stehen in jeder Zeile die drei Koordinaten (x,y,z). Z.B. :
12.222 -1.01 13.4
34 23.3 -17.93
...Jeder dieser Punkte gibt eine Ecke des Kantenzuges an. Die Kanten sind die geradlinigen Verbindungen der Ecken. Vom letzten Punkt des Kantenzuges fÞhrt wieder eine Kante zum ersten, um den Kantenzug zu schlieÃen.
Die erste Ecke wird nicht nochmal am Ende der Datei angegeben. Es kÃķnnen beliebig viele Freizeichen oder Tabs zwischen zwei Zahlen vorkommen. Wichtig ist nur, dass pro Zeile nur drei Zahlen stehen. Der eingelesene Kantenzug soll nun verrastert werden, das heiÃt, er soll in ganzzahlige Koordinaten (die sogenannten Voxel) konvertiert werden.
Abbildung 4: Verrasterte Kante von (0,0,0) nach (12,5,0)
Hierbei ist darauf zu achten, dass entlang des Kantenzuges zwei benachbarte Voxel immer Þber eine gemeinsame SeitenflÃĪche benachbart sind. Die Voxel um (0,0,0) und (1,1,1) sind demnach nicht benachbart, sondern kÃķnnen z.B. so verbunden werden:
(0, 0, 0)
(1, 0, 0)
(1, 1, 0)
(1, 1, 1)

Um z.B. die Verbindungsstrecke zwischen (-24, 11, 15) und (33,45,-23) zu verrastern, ist es sinnvoll, das Problem zunÃĪchst in der xy-Ebene zu lÃķsen, und im zweiten Schritt die z-Komponente zu bearbeiten. Dabei mÞssen dann evtl. neue Voxel eingefÞgt werden. Die Voxel-Daten sollen in eine Text-Datei gespeichert werden (drei Integer pro Zeile fÞr die drei Koordinaten eines jeden Voxel). AuÃerdem sollen solche Dateien auch eingelesen werden kÃķnnen. Das Programm soll erkennen, wenn zwei Kanten zu nah beieinander liegen, damit nach dem Vervoxeln keine BerÞhrungen verschiedener Kanten stattfinden und immer klar bleibt, in welcher Reihenfolge die Voxel durchlaufen werden.
-
Es soll ein gegebener Knoten eingelesen werden. Der Knoten wird als ein Link (s.o.) betrachtet, indem wir die z-Achse als Teil eines zweiten (Un-)knotens auffassen, der entlang der z-Achse lÃĪuft, dann einmal ganz auÃen um den ersten Knoten herum und von der negativen z-Achse wieder entlang der z-Richtung durch den ersten Knoten hindurch. Dieser zweite Knoten wird nicht in der Datei mit angegeben oder extra eingelesen, sondern er existiert nur implizit innerhalb des Programms bzw. innerhalb der nÃķtigen Algorithmen. Auf diese Weise vereinfacht sich das Datenformat und die Darstellung erheblich.


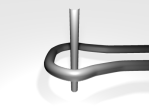
Abbildung 5: a) Link b) z-Achse als Stange c) SchlaufenentfernungEs soll nun entweder im Voxel-Modell oder im Kantenzug versucht werden, einen Link zu vereinfachen, indem z.B. ÞberflÞssige Schlaufen abgeschnitten werden. Dabei mÞssen verlinkte Knoten nach dem Entfernen einer Schlaufe immernoch verlinkt bleiben. In Abb. 4c z.B. kann alles rechts auÃerhalb des Bildes abgeschnitten werden. Die offenen Enden werden dann verbunden.
-
Das Programm soll nun versuchen festzustellen, ob der vereinfachte Link wirklich verlinkt ist, oder ob sich die beiden Knoten separieren lassen. Sollte dies nicht fÞr alle Links mÃķglich sein, muss angegeben werden fÞr welche Klasse bzw. SonderfÃĪlle von Links das Programm die Verlinktheit feststellen kann, bzw. fÞr welche FÃĪlle eine Feststellung der Verlinktheit fehlschlÃĪgt.


Abbildung 6: a) separierbar b) nicht separierbar
Teilnahmebedingungen
Anmeldeschluss ist der 20.12.03.
Gruppenmeldungen sind nicht mÃķglich.
Als Programmiersprache sind Pascal, C, C++ und Java zugelassen. Die Sprache muss bei der Anmeldung mit angegeben werden. Es dÞrfen nur die Standard-Bibliotheken und keine Codegeneratoren verwendet werden.
Es muss eine 5 bis 10-seitige Ausarbeitung angefertigt werden, in der die benutzten Algorithmen erklÃĪrt werden, und in der das Programm ausfÞhrlich dokumentiert wird.
Das erstellte Programm und die Ausarbeitung sowie ein Ausdruck eines Testdurchlaufs bzw. die Ergebnisse mit von uns gestellten Daten sind spÃĪtestens bis zum 16.02.04 bei uns einzureichen.
Es dÞrfen nur SchÞler der Sekundarstufe I oder II allgemeinbildender Schulen aus Niedersachsen an dem Wettbewerb teilnehmen. FamilienangehÃķrige von Mitarbeitern des Fachgebietes Graphische Datenverarbeitung an der UniversitÃĪt Hannover sind leider ausgeschlossen.
Der Rechtsweg ist ausgeschlossen.
Bewertungskriterien
LauffÃĪhigkeit und Korrektheit des Programms
Gut verstÃĪndliche Dokumentation der Algorithmen ggf. mit Ergebnissen von Beispieldaten
Besondere eigenstÃĪndige Ideen
In ZweifelsfÃĪllen: Strukturierter Programmierstil
So, das war's erstmal. Hoffentlich hast Du ein wenig Lust bekommen, bei diesem Gewinnspiel mitzumachen. Es geht bei dieser Competition nicht darum, alles perfekt zu machen. Wir freuen uns auch Þber TeillÃķsungen. Wenn wir merken, dass Du Dich mit der Problematik beschÃĪftigt hast, hier und da ein paar interessante eigene Ideen hattest und Deine Gedanken und Algorithmen dokumentierst, hast Du gute Chancen unter den drei Besten zu sein. Bei RÞckfragen kannst Du Dich gerne bei uns melden.
E-Mail: competition(at)gdv.uni-hannover.de
Viel Erfolg,
i.A. Dipl. - Math. Martin Reuter
Lehrstuhl Graphische Datenverarbeitung
Prof. Dr. F. - E. Wolter

