Randflächenrekonstruktion von Volumenkörpern anhand diskreter Daten

Karl-Ingo Friese, Leibniz Universität Hannover, Diplomarbeit
01/2000

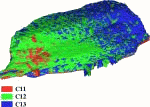
Die Rekonstruktion von Volumenkörpern spielt in der Computergrafik eine entscheidende Rolle. Sei es der Kopf eines Schauspielers, der für die Spezialeffekte in einem neuen Kinofilm erfaßt wird, ein Bauteil, das nach der Fertigung vermessen und mit dem 'virtuellen Prototyp' verglichen werden soll. Sei es ein Gebäude, ein Industriekomplex oder - wie in diesem Fall - eine Höhle, die als physisches Objekt gegeben ist und nun vermessen
und im Computer dargestellt werden soll.

Bijan Farajollahi hat in seiner Arbeit Verfahren zur Bereinigung der Meßfehler, zur Elimination 'überflüssiger' Meßpunkte, sowie ein Verfahren, das jede Messung für sich trianguliert vorgestellt. Die Triangulation der einzelnen Messung ist für diese Arbeit als gelöst vorausgesetzt.

An dieser Stelle gibt es zwei Möglichkeiten, wie man fortfahren könnte. Entweder man faßt alle Meßpunkte zusammen, bereinigt die Fehler und versucht dann die entstandene Punktwolke zu triangulieren - oder man trianguliert jede Messung für sich und vereinigt die so entstandenen Flächen zu einer einzigen. In dieser Arbeit soll das zweite Verfahren behandelt werden; die Vereinigung von einfachen, geschlossenen Dreiecksflächen.

Anschaulich betrachtet bedeutet dies, daß hierfür die kleinste, umschließende Hülle gefunden werden muß, also die Dreiecksfläche, die alle eingeschlossenen Punkte von beiden Ausgangsflächen enthält.

Kontakt: Franz-Erich Wolter