Dreidimensionale Dynamische Voronoi-Diagramme

Richard Algaier, Leibniz Universität Hannover, Studienarbeit
10/2008

Das Voronoi-Diagramm ist ein in vielen Bereichen genutztes fundamentales Konzept der berechnenden Geometrie.

Ausgehend von einer endlichen Menge von Punkten (Orte) wird mit Hilfe der Distanzfunktion eine Partitionierung des Raumes erzeugt, die eine Reihe interessanter Eigenschaften hat. Die Berechnung des Voronoi-Diagramms bzw. der dualen Delaunay-Triangulation kann in O(n log n) geschehen. Verfahren zur Berechnung sind z.B. Divide-and-Conquer oder inkrementelle randomisierte Algorithmen.

Bewegt man eine Untermenge der Orte, so verändert sich die Struktur des Voronoi-Diagramms, wobei Anderungen der Topologie auftreten können.

Ziel dieser Arbeit ist es, für einen Spezialfall sich bewegender Orte einen Algorithmus zu entwickeln
und zu implementieren, der das Voronoi-Diagramm im dreidimensionalen Euklidischen Raum
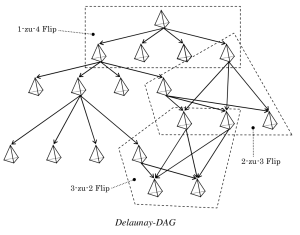
adaptiv berechnet. Der betrachtete Spezialfall besteht in einer Aufteilung der Ortsmenge in zwei Untermengen, wobei die eine Menge durch eine Translation bewegt wird. Das Voronoi-Diagramm muss in diesem Falle nicht komplett neu berechnet werden, sondern nur zum Teil, indem man einen Gerichteten Azyklischen Graphen, den sogenannten Delaunay-DAG verwendet.

Kontakt: Philipp Blanke