Eine Datenstruktur für Atlanten zur FEM-Berechnung

Christian Schlüter, Leibniz Universität Hannover, Studienarbeit
01/2002

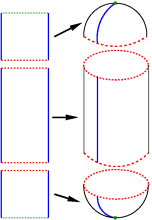
Die Erstellung beliebiger Flächen und das Aufstellen geeigneter Triangulierungen, für die möglichst genaue Berechnung der Schwingungsspektren der Flächen mit Hilfe des Laplace - Beltrami - Operators ist im Allgemeinen sehr schwierig. Ein intuitiver Ansatz ist die Komposition einer Fläche aus mehreren Teilflächen, die eine einfachere Darstellung besitzen und deren Triangulierung an das Gesamtproblem angepasst werden kann. Das Ziel dieser Arbeit ist das Zusammenfügen (im folgenden Verschweissen genannt) beliebiger Flächen zu einer neuen Fläche. Auf dieser Fläche soll die Eigenwertberechnung des Laplace - Beltrami - Operators möglich sein.

Zur genaueren Berechnung sollen ferner auch eine Verfeinerung bzw. das Anlegen höhergradiger Finiter - Elemente möglich sein. Ein weiterer Aspekt ist die Verbesserung des globalen Indexes (Sortierung der vorhandenen Flächenpunkte). Dadurch wird zum einen der Speicherplatzbedarf zur Berechnung des Laplace - Beltrami - Operators verringert und zum anderen auch dessen Berechnungszeit verkürzt.

Kontakt: Martin Reuter