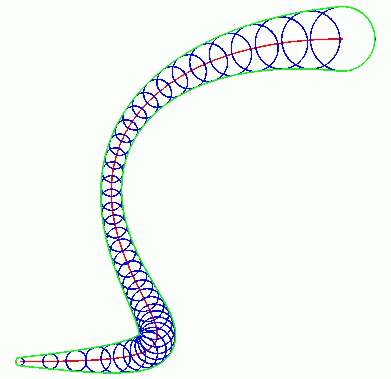
Medial axis (in red) of a curved planar
tubular-like object .
By definition, the medial axis contains all centers of maximally
inscribed disks (in blue).
The envelope of this set of disks (re-)generates the original object
boundary (in green).
Feb. 2000
The sample pictures shown here are adapted from several Master's theses of some of Prof. Wolter`s students in Hannover. The students involved in preparing the figures displayed here include A. Howind (curved boundary shape cases), P. v. Grumbkow (piecewise linear boundary case) R. Kunze (Geodesic Voronoi Diagrams), M. Baer (Geodesic Medial Axis).
This page:

Medial axis (in red) of a curved planar
tubular-like object .
By definition, the medial axis contains all centers of maximally
inscribed disks (in blue).
The envelope of this set of disks (re-)generates the original object
boundary (in green).
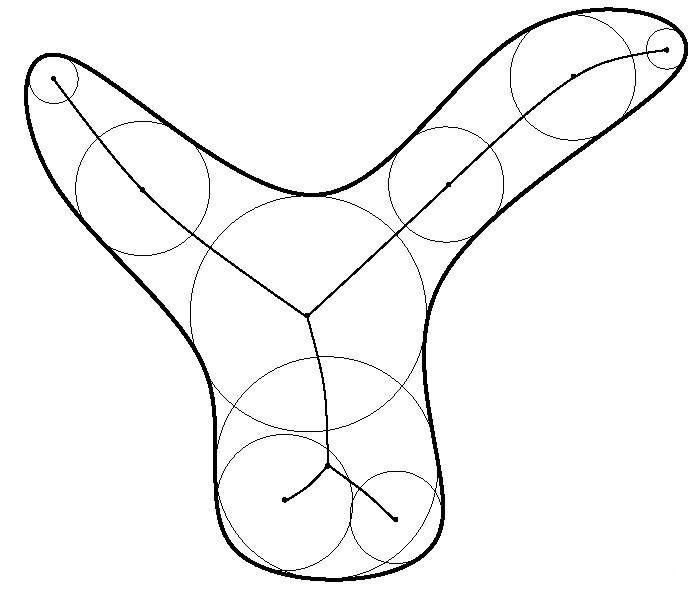
Medial axis of a curved object in the plane;
some of the associated maximally inscribed circles are also shown.
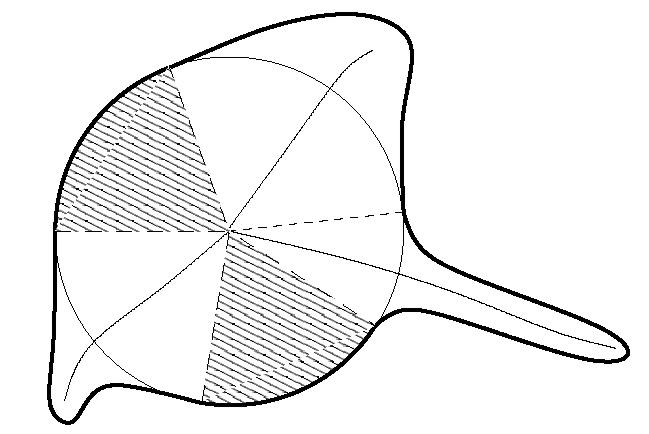
Medial axis of a curved object in the plane;
special case with simultaneous finite contact at two circular arcs.
|
|
|
| Shows yellow-orange colored spheres of maximal size that are contained in B. Those spheres typically (but not always) touch the boundary surface of B. The set containing all centers of those spheres of maximal size defines the Medial Axis of the solid B. This medial axis in this example is (a rectangular surface patch). | The shape of the medial axis of the solid B is indicated by the red colored boundary curve of the surface patch being the medial axis of B. | Displays in blue color the boundary surface parts of the solid B. Those boundary surfaces can be understood to constructed as envelope surfaces of the family of maximal sphere shown in the first picture of this sequence. |
|
|
| Shows with green color the boundary curves of the medial axis of a disc like solid D whose boundary is defined here by triangular facets the edges of which are the black line segments describing the solids boundary surface by a wireframe model. The medial axis of D is given here by a collection of two-dimensional surface sheets whose boundary edges are green. Those edges have red vertices. | With the same usage of colors as in the figure on the left, we display the Medial Axis of Solid T. The boundary surface of T (indicated by the black wireframe model) is topologically a torus surface. |