Feb. 2000

Cut Locus and Medial Axis in the Euclidean Space and on Surfaces

by Professor Franz-Erich WOLTER

Illustrative Figures - Cont'd

This page:

Geodesic Voronoi diagrams

Geodesic Case - Voronoi Diagram on Curved Surfaces

These pictures describing geodesic Voronoi Diagrams on surfaces are from R. Kunze Master's thesis; cf. they also appear in the downloadable paper "Welfen Lab. Rep. 2".

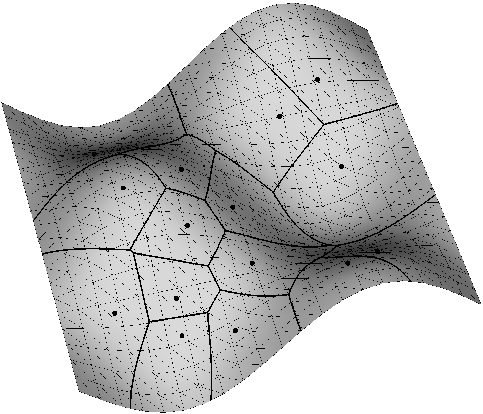
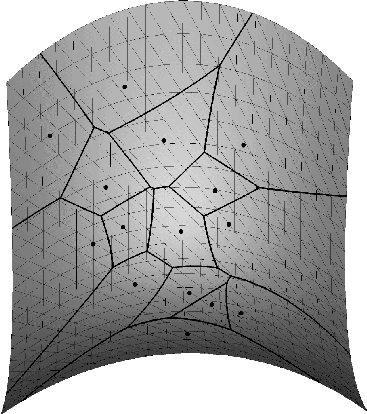
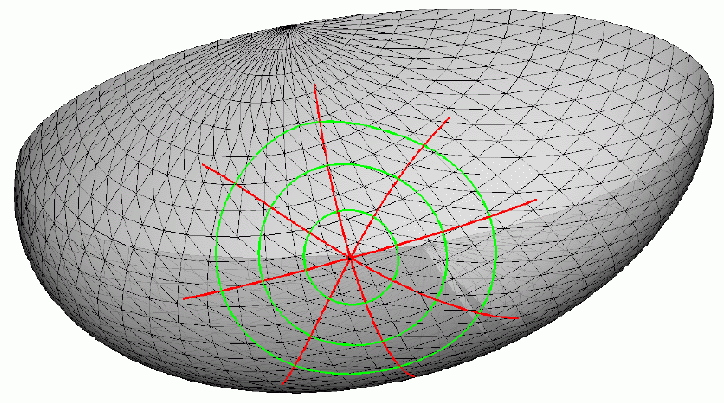
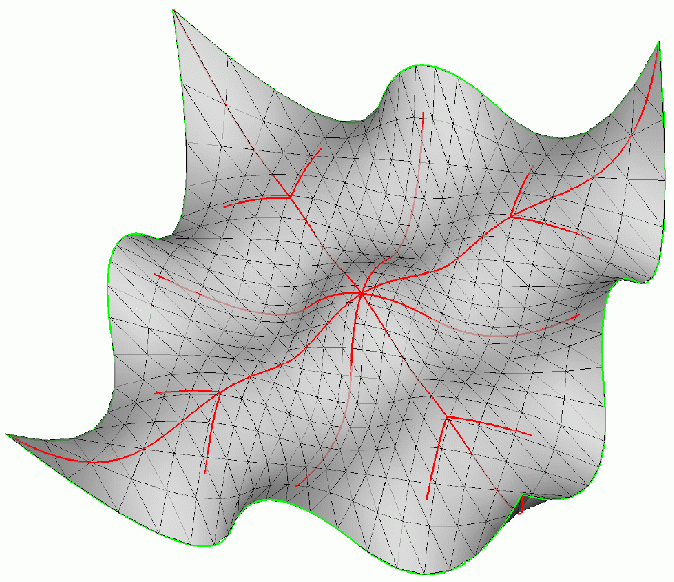
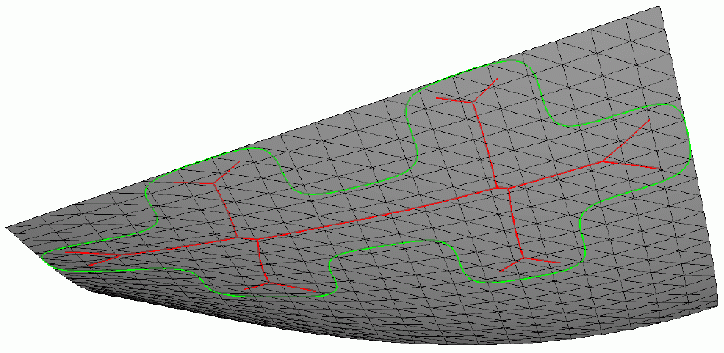
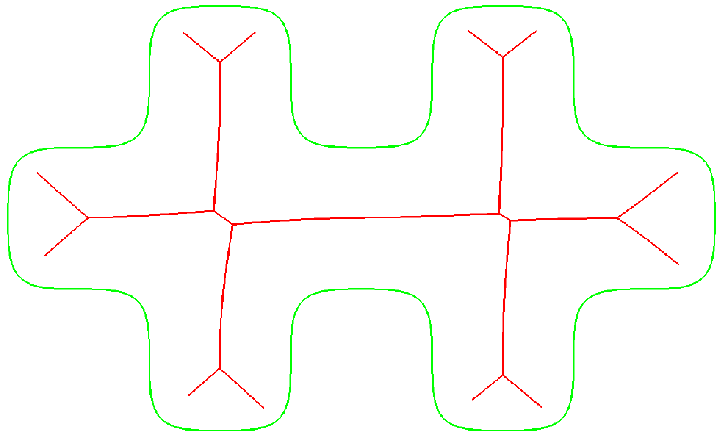
Shows the Geodesic Voronoi Diagram with respect to the finite point set P (given by the black dots) on the wave-like shaped surface S. This geodesic Voronoi diagram is given by the black edges. Each of those edges consists of points that are (geodesically) equidistant with respect to two (specific) points of the discrete set S. Here the geodesic distance between two given surface points is defined by the minimal length of all surface curves joining the two given points. As in the Euclidean case the geodesic Voronoi diagram partitions the surface into separate open domains. Each of those open domains contains exactly one point p of P. Together with p, the respective open domain contains all surface points whose geodesic distance to p is smaller than to any other point in the set P.	With the same conventions as in the previous wave like surface (figure on the left) we display now the geodesic Voronoi diagram of a finite point set located on a hyperbolic paraboloid surface

Geodesic Case: Medial Axis on Curved Surfaces

These two figures illustrate the tree-like structure of the geodesic medial axis on curved surface patches. The shape of these patches resemble that of hilly landscapes. The **dark** curves depict both the boundaries of these surface patches, and the geodesic medial axes that are here topological trees. In analogy to the Euclidean situation, every point of the geodesic medial axis on a bordered surface B is the center of a geodesic disc of maximal size that is still contained in B. On any surface S a geodesic disc *D(p,r)* with center p and radius r contains all points on S whose (minimal) geodesic distance to p is smaller or equal to r. The minimal geodesic distance between two points p & q on a surface S is defined by the minimal length of all curves in S that join p and q.

Example of geodesic circles (distance gauge figure) by T. Rausch. It shows in red some geodesics (locally shortest surface curves) emanating from a surface point. The latter is the center of a system of concentric "circles" on the surface depicted in green. Here, each such (3D) circle contains points at a fixed (geodesic) distance to the center.


Geodesic Medial Axis (in red ) on a surface patch (boundaries in green ). This surface is defined on a rectangular parameter domain.	Back-projection in the rectangular parameterization domain containing the initial surface boundaries (in green ) and the computed geodesic medial axis (in red ).


Geodesic Medial Axis (in red ) for a surface patch (boundaries in green ) contained within a larger curved surface (a rational B-spline here).	Back-projection in a rectangular parameterization domain containing the initial (sub)surface boundaries (in green ) and the computed geodesic medial axis (in red ).

BACK UP NEXT

Last Updated: Feb. 5, 2000